Corriente Alterna
Se denomina corriente alterna (abreviada CA en español y AC en inglés, de alternating current) a la corriente eléctrica en la que la magnitud y el sentido varían cíclicamente. La forma de oscilación de la corriente alterna más comúnmente utilizada es la de una oscilación senoidal (figura 1), puesto que se consigue una transmisión más eficiente de la energía. Sin embargo, en ciertas aplicaciones se utilizan otras formas de oscilación periódicas, tales como la triangular o la cuadrada.
Utilizada genéricamente, la CA se refiere a la forma en la cual la electricidad llega a los hogares y a las industrias. Sin embargo, las señales de audio y de radiotransmitidas por los cables eléctricos, son también ejemplos de corriente alterna. En estos usos, el fin más importante suele ser la transmisión y recuperación de la información codificada (o modulada) sobre la señal de la CA.
Características
Frecuencia
La frecuencia de la corriente alterna (C.A.) constituye un fenómeno físico que se repite cíclicamente un número determinado de veces durante un segundo de tiempo y puede abarcar desde uno hasta millones de ciclos por segundo o hertz (Hz).
|
 | ||
En esta ilustración se puede observar a la izquierda, la representación gráfica de una onda sinusoidal de. corriente alterna con una frecuencia de un ciclo por segundo o hertz, mientras que a la derecha aparece.. la misma onda, pero ahora con cinco ciclos por segundo de frecuencia o hertz. | ||
La frecuencia se representa con la letra ( f ) y su unidad de medida es el ciclo por segundo o hertz (Hz). Sus múltiplos más generalmente empleados son los siguientes: |
|
La corriente alterna puede tener diferentes formas de onda, pero la más común es la que presenta una onda sinusoidal o senoidal por cada ciclo de frecuencia.
Periodo
Tiempo necesario para que un ciclo se repita. Se mide en segundos y se representa con la letra P.
Frecuencia y periodo son valores inversos T =1/f f =1/T  |
Amplitud
Amplitud de la corriente alterna. En la Corriente alterna la magnitud y dirección varían cíclicamente. La Onda senoidal representa el valor de la tensión a través del tiempo y no se puede establecer el valor de la misma sin definir qué momento es válido, ya que a través del tiempo es continuamente variable. Por ello se toma el valor pico, el valor eficaz y el valor medio.

Longitud De Onda
Aunque cada uno de los electrones que integran la corriente eléctrica recorren un conductor en forma relativamente lenta, el campo eléctrico o impulso que produce el flujo de corriente, avanza en un conductor aproximadamente a 300,000 kilómetros por segundo. Puesto que la corriente avanza a una velocidad definida, sólo puede recorrer cierta distancia durante determinado tiempo. Y puesto que la frecuencia en realidad es una medida del número de ciclos por determinado tiempo, es posible calcular hasta dónde puede llegar la corriente durante un ciclo de tensión alterna. Esta distancia recibe el nombre de longitud de onda y es la distancia que puede recorrer la corriente en el tiempo que requiere la terminación de un ciclo completo de tensión alterna.
En una tensión de 60 cps, por ejemplo, un ciclo tarda un sesentavo de segundo. Y, puesto que la corriente recorre 300,000 kilómetros en un segundo, sólo puede avanzar 5,000 kilómetros. Puesto que la longitud de onda de una tensión alterna depende de su frecuencia y de la velocidad con la que el impulso eléctrico recorre el conductor, se puede calcular según la siguiente ecuación:
Longitud de onda = velocidad de la corriente/frecuencia
Por lo que respecta a la electricidad básica la velocidad de la corriente es igual a la velocidad de la luz: 300,000 kilómetros por segundo. Entonces, la ecuación para la longitud de onda será:
Longitud de onda (metros) = 300.000,000/frecuencia
La longitud de onda para un ciclo de una tensión 60 cps será pues de 5.000,000 de metros.
Así, pues, Longitud de onda es sólo otra forma de expresar la frecuencia. La longitud de onda no es muy importante en aplicaciones de potencia eléctrica pero suele tener aplicación en el campo de las comunicaciones.
Ciclo
se llama ciclo a toda forma de onda que completa una forma, es decir comienza en un punto de la forma de onda y termina el mismo punto para iniciar otro ciclo.
Fase
La salida de un generador simple de c-a varia en forma de onda sinusoidal. Por lo tanto, si dos de estos generadores se ponen a funcionar, cada uno generará una salida sinusoidal completa después de una revolución. Si los generadores se hacen funcionar en elmismo instante y giran exactamente a la misma velocidad, las dos formas de onda comenzarán y terminarán simultáneamente. También alcanzarán sus valores máximos y pasarán por cero al mismo tiempo. Entonces se dice que las dos formas de onda “coinciden” entre sí y que las tensiones que representan están en fase. De aquí se concluye que el término fase se usa para indicar la relación de tiempo entre tensiones y corrientes alternas.
El que dos corrientes o tensiones estén en fase no significa que sus magnitudes sean iguales. Las magnitudes máximas se alcanzan al mismo tiempo, pero sus valores pueden ser diferentes.
Aunque generalmente se usa el término fase para comparar la relación de tiempo de dos ondas, también se puede usar para indicar un punto de una onda en determinado instante.
Desfase o Diferencia De Fase
Si dos generadores idénticos arrancan al mismo tiempo y giran a la misma velocidad, sus valores máximo y mínimo ocurrirán simultáneamente, de manera que ambas salidas estarán en fase. Pero si un generador se arranca después del otro, sus valores máximo y mínimo de salida ocurrirán después de los valores correspondientes al otro generador. En el caso que se considera, ambas salidas están de basados, o, dicho de otra manera, existe una diferencia de fase entre ambas salidas. La magnitud de la diferencia de fase depende de cuánto atraso tenga una salida con respecto a la otra.
La diferencia de fase se puede expresar en fracciones de ciclo. Luego. si una salida comienza cuando la otra acaba de completar la mitad de un ciclo, la diferencia de fase es de medio ciclo, sin embargo, la diferencia de fase se mide generalmente en grados para mayor precisión. Y puesto que una onda sinusoidal completa corresponde a 360 grados. una diferencia de fase de medio ciclo será una diferencia de fase de 180 grados: una diferencia de fase de un cuarto de ciclo será una diferencia de 90 grados
Los términos adelantado y atrasado se usan para definir las posiciones relativas en el tiempo, de dos tensiones o corrientes que estén fuera de fase. La que está adelante en el tiempo, se dice que está adelantada, en tanto que la otra estará atrasada.
Valores Instantaneos
El valor instantáneo de una señal de corriente alterna es cualquier punto de esa señal alterna. O dicho de otra manera mas técnica, es el valor que se obtiene en cada instante de tiempo en la función senoidal.
Valores Pico
La señal tiene dos valores picos.Uno es positivo y el otro negativo, pues cada uno de ellos corresponde a un semiciclo de la señal. Ahora bien, el valor maximo o valor pico es el mayor de esos dos valores picos que tiene un ciclo de señal senoidal, independientemente si es positivo o negativo.
Existe otro concepto, el de valor pico-pico. Como se puede imaginar en este concepto se abarca los dos semiciclos, es decir, seria la distancia que hay entre las dos crestas de la señal, la positiva y la negativa.
Valores Efectivos
Aunque los valores medios de una tensión o una corriente alternas son útiles, no tienen relación con valores correspondientes en c-c. Puede saberse que en un circuito fluye una corriente alterna cuyo valor medio es 10 amperes, pero esto no proporciona información sobre cómo se compararía con 10 amperes de c-c en el mismo circuito. Puesto que muchos equipos eléctricos tienen circuitos tanto de c-a como de c-c, es muy útil si se pueden expresar corrientes y tensiones alternas en valores que se relacionen con c-c. Es posible hacer esto gracias al uso de valores efectivos.
El valor efectivo de una tensión o corriente alterna es el que, en un circuito que sólo contenga resistencia, produce la misma cantidad de calor que la producida por una tensión o corriente continua del mismo valor. Por lo tanto, una corriente alterna cuyo valor eficaz sea de 1 ampere, genera el mismo calor en una resistencia de 10 ohms que una comente directa de 1 ampere. El valor efectivo también se llama raíz cuadrático media, o rom, debido a la forma en que se obtiene: es igual a la raíz cuadrada del valor medio de los cuadrados de todos los valores instantáneos de corriente o tensión, durante medio ciclo.
En una onda sinusoidal pura, el valor efectivo es 0.707 veces el valor pico. Por lo tanto, las ecuaciones para calcular los valores efectivos de corriente y tensión son las siguientes:
EEF = 0.707pico EEF = 0.707 pico
Por lo tanto, para una tensión pico de 100 volts el valor rcm de una tensión alterna seria 70.7 volts. Esto significa que un resistor conectado a una fuente de c-a de 100 volts, producirá el mismo calor que si se colocara en una fuente de c-c de 70.7 volts.
El valor efectivo se usa para clasificar tensiones y corrientes alternas. La tensión de 110 volts que llega a los hogares es el valor rcm.También lo es la tensión de potencia de 220 volts para usos industriales.
Valor eficaz de una señal de corriente o voltaje con offset
Valores Eficaz
En electricidad y electrónica, en corriente alterna, el valor cuadrático medio (en inglés root mean square, abreviado RMS o rms), de una corriente variable es denominado valor eficaz. Se define como el valor de una corriente rigurosamente constante (corriente continua) que al circular por una determinada resistencia óhmica pura produce los mismos efectos caloríficos (igual potencia disipada) que dicha corriente variable (corriente alterna). De esa forma una corriente eficaz es capaz de producir el mismo trabajo que su valor en corriente directa o continua. Como se podrá observar derivado de las ecuaciones siguientes, el valor eficaz es independiente de la frecuencia o periodo de la señal.
Al ser la intensidad de esta corriente variable una función continua i(t) se puede calcular:
donde:
 es el periodo de la señal.
es el periodo de la señal.
Esta expresión es válida para cualquier forma de onda, sea ésta sinusoidal o no, siendo por tanto aplicable a señales de radiofrecuencia y de audio o vídeo.
En el caso de una corriente alterna sinusoidal (como lo es, con bastante aproximación, la de la red eléctrica) con una amplitud máxima o de pico Imax, el valor eficaz Ief es:
En el caso de una señal triangular con una amplitud máxima Imax, el valor eficaz Ief es:
Para una señal cuadrada es:
Para el cálculo de potencias eficaces Pef por ser proporcional con el cuadrado de la amplitud de la tensión eléctrica, para el caso de señales sinusoidales se tiene:
Del mismo modo para señales triangulares:
Es común el uso del valor eficaz para voltajes también y su definición es equivalente:
Valor eficaz de una señal de corriente o voltaje con offset
En ocasiones una señal de corriente o voltaje posee un componente de continua, que se le suele llamar offset, que implica un desplazamiento hacia arriba o hacia abajo de la forma
donde a puede ser positivo o negativo, positivo si se desplaza hacia arriba y negativo si se desplaza hacia abajo.
Su valor efectivo en caso de ser senoidal será:
en caso de ser triangular:
en caso de ser cuadrada:
Valores Medios
El valor medio de una tensión o una corriente alternas es el promedio de todos los valores instantáneos durante medio ciclo, o sea, una alternación. Puesto que durante medio ciclo la tensión o la corriente aumentan de cero al valor pico y luego disminuyen a cero, el valor promedio debe encontrarse en algún punto entre cero y el valor pico. Para una onda sinusoidal pura, que es la forma de onda más común en los circuitos de c-a, el valor promedio es 0.637 veces el valor pico. Para tensión. esto se expresa mediante la ecuación:
EMED = 0.637 pico
Por ejemplo. si la tensión pico de un circuito es de 100 volts, la tensión media será:
EMED = 0.637 ~ = 0.637 X lOO = 63.7 volts
La ecuación para calcular la corriente media en función de corriente pico es idéntica a la que se dio para el caso de la tensión.
Debe tenerse cuidado de no confundir el valor medio, que es el promedio de medio ciclo, con el promedio de un ciclo completo. Puesto que ambos medios ciclos son idénticos, excepto porque uno es positivo y el otro negativo, el promedio sobre un ciclo completo, seria cero.
Factor De Potencia
El llamado triángulo de potencias es la mejor forma de ver y comprender de forma gráfica qué es el factor de potencia o coseno de “fi” (Cos
|
 |
Como se podrá observar en el triángulo de la ilustración, el factor de potencia o coseno de “fi” (Cos |
 |
El resultado de esta operación será “1” o un número fraccionario menor que “1” en dependencia del factor de potencia que le corresponde a cada equipo o dispositivo en específico, según contenga un circuito inductivo, resistivo, o una combinación de ambos. Ese número responde al valor de la función trigonométrica “coseno”, equivalente a los grados del ángulo que se forma entre las potencias (P) y (S). Si el número que se obtiene como resultado de la operación matemática es un decimal menor que “1” (como por ejemplo 0,95), dicho número representará el factor de potencia correspondiente al defasaje en grados existente entre la intensidad de la corriente eléctrica y la tensión o voltaje en el circuito de corriente alterna. Lo «ideal» sería que el resultado fuera siempre igual a “1”, pues así habría una mejor optimización y aprovechamiento del consumo de energía eléctrica, o sea, habría menos pérdida de energía no aprovechada y una mayor eficiencia de trabajo en los generadores que producen esa energía. Sin embargo, un circuito inductivo en ningún caso alcanza factor de potencia igual a "1", aunque se empleen capacitores para corregir completamente el desfasaje que se crea entre la potencia activa (P) y la aparente (S). Al contrario de lo que ocurre con los circuitos inductivos, en aquellos que solo poseen resistencia activa, el factor de potencia sí será siempre igual a “1”, porque como ya vimos anteriormente en ese caso no se crea ningún desfasaje entre la intensidad de la corriente y la tensión o voltaje.
En los circuitos inductivos, como ocurre con los motores, transformadores de voltaje y la mayoría de los dispositivos o aparatos que trabajan con algún tipo de enrollado o bobina, el valor del factor de potencia se muestra siempre con una fracción decimal menor que “1” (como por ejemplo 0,8), que es la forma de indicar cuál es el retraso o desfasaje que produce la carga inductiva en la sinusoide correspondiente a la intensidad de la corriente con respecto a la sinusoide de la tensión o voltaje. Por tanto, un motor de corriente alterna con un factor de potencia o Cos
Corrección Del Factor Potencia
A menudo es posible ajustar el factor de potencia de un sistema a un valor muy próximo a la unidad.
Esta práctica es conocida como mejora o corrección del factor de potencia y se realiza mediante la conexión a través de conmutadores, en general automáticos, de bancos de condensadores o de inductancias, según sea el caso el tipo de cargas que tenga la instalación. Por ejemplo, el efecto inductivo de las cargas de motores puede ser corregido localmente mediante la conexión de condensadores. En determinadas ocasiones pueden instalarse motores síncronos con los que se puede inyectar potencia capacitiva o reactiva con tan solo variar la corriente de excitación del motor.
Las pérdidas de energía en las líneas de transporte de energía eléctrica aumentan con el incremento de la intensidad. Como se ha comprobado, cuanto más bajo sea el f.d.p. de una carga, se requiere más corriente para conseguir la misma cantidad de energía útil. Por tanto, como ya se ha comentado, las compañías suministradoras de electricidad, para conseguir una mayor eficiencia de su red, requieren que los usuarios, especialmente aquellos que utilizan grandes potencias, mantengan los factores de potencia de sus respectivas cargas dentro de límites especificados, estando sujetos, de lo contrario, a pagos adicionales por energía reactiva.
La mejora del factor de potencia debe ser realizada de una forma cuidadosa con objeto de mantenerlo lo más alto posible. Es por ello que en los casos de grandes variaciones en la composición de la carga es preferible que la corrección se realice por medios automáticos.
Supongamos una instalación de tipo inductivo cuyas potencias P, Q y S forma el triángulo de la figura 1. Si se desea mejora el cosφ a otro mejor cosφ', sin variar la potencia activa P, se deberán conectar un banco de condensadores en paralelo a la entrada de la instalación para generar una potencia reactiva Qc de signo contrario al de Q, para así obtener una potencia reactiva final Qf. Analíticamente:
Por un lado
y análogamente
Luego,
donde ω es la pulsación y C la capacidad de la batería de condensadores que permitirá la mejora del f.d.p. al valor deseado. Sustituyendo en la primera igualdad,
de donde
|
Coseno
Un motor de 500 KVA funciona a plena carga con un factor de potencia de 0,6. Añadiendo capacitores se modifica dicho factor pasando a valer 0,9. Hallar la potencia reactiva de los capacitores necesarios. Realizar la gráfica con dicha corrección. Frecuencia = 50 Hertz. Tensión = 380 V
|
En un circuito RL serie en corriente alterna, se tiene una resistencia y una bobina en serie. La corriente en ambos elementos es la misma.
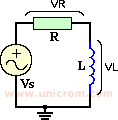
La tensión en la bobina está en fase con la corriente (corriente alterna) que pasa por ella (tienen sus valores máximos simultáneamente).
Pero el voltaje en la bobina está adelantado a la corriente que pasa por ella en 90º (la tensión tiene su valor máximo antes que la corriente)
El valor de la fuente de voltaje que alimenta este circuito esta dado por las siguientes fórmulas:
- Voltaje (magnitud) VS = (VR2 + VL2)1/2 - Angulo = /Θ = Arctang (Vl/VR).
Estos valores se expresan en forma demagnitud y ángulo. Ver el diagramafasorial de tensiones

Ejemplo: 47 /30° que significa que tiene magnitud de 47 y ángulo de 30 grados
La impedancia Z sería la suma (suma fasiorial) de la resistencia y la reactancia inductiva. Y se puede calcular con ayuda de la siguiente fórmula:
Para obtener la magnitud de Z de dividen los valores de Vs e I
Para obtener el /Θ de Z se resta el ángulo de la corriente, del ángulo del voltaje.
Nota: lo que está incluido en paréntesis elevado a la 1/2, equivale a la raíz cuadrada.
Circuito RL En Paralelo
En un circuito RL paralelo, el valor devoltaje es el mismo para la resistenciay para la bobina. Ver el siguiente diagrama

V = VR = VL
La corriente que pasa por la resistencia está en fase con el voltaje aplicado. (El valor máximo de voltaje coincide con el valor máximo de corriente).
En cambio en la bobina la corriente se atrasa 90º con respecto al voltaje. (el valor máximo devoltaje sucede antes que el valor máximo de la corriente)

La corriente total que alimenta este circuito se puede obtener con ayuda de las siguientes fórmulas:
- Corriente (magnitud) It = (IR2 + IL2)1/2
- Angulo Θ = Arctang (-IL/IR)
Ver el diagrama fasorial y de corrientes

La impedancia (Z) se obtiene con ayuda de la siguiente fórmula:
¿Cómo se logra lo anterior?
- Para obtener la magnitud de Z dividen las magnitudes de Vs e It para obtener la magnitud de la impedancia
- Para obtener el /Θ de Z se resta el ángulo de la corriente del de voltaje para obtener el ángulo de la impedancia.
Nota: lo que está incluido en paréntesis elevado a la 1/2, equivale a la raíz cuadrada.
|
Circuito RC En Serie
En un circuito RC en serie la corriente (corriente alterna) que pasa por la resistor y por el capacitor es la misma
El voltaje entregado VS es igual a la suma fasorial de la caída de voltaje en el resistor(Vr) y de la caìda de voltaje en el capacitor (Vc). Ver la siguiente fórmula: Vs = Vr + Vc (suma fasorial)

Esto significa que cuando la corriente está en su punto más alto (corriente pico), será así tanto en el resistor como en el capacitor.
Pero algo diferente pasa con los voltajes. En el resistor, el voltaje y la corriente están en fase (sus valores máximos y mínimos coinciden en el tiempo). Pero el voltaje en el capacitor no es así.
Como el capacitor se opone a cambios bruscos de voltaje, el voltaje en elcapacitor está retrasado con respecto a la corriente que pasa por él. (el valor máximo de voltaje en el capacitor sucede después del valor máximo de corriente en 90o).
Estos 90º equivalen a ¼ de la longitud de onda dada por la frecuencia de la corriente que está pasando por el circuito.
El voltaje total que alimenta el circuito RC en serie es igual a la suma fasorial del voltaje en el resistor y el voltaje en elcapacitor.
Este voltaje tiene un ángulo de desfase (causado por el capacitor) y se obtiene con ayuda de las siguientes fórmulas:
Valor del voltaje (magnitud): Vs = ( VR2 + VC2 )1/2
Angulo de desfase Θ = Arctang (-VC/VR)
Angulo de desfase Θ = Arctang (-VC/VR)
Como se dijo antes
- La corriente adelanta al voltaje en un capacitor en 90°
- La corriente y el voltaje están en fase en un resistor.
- La corriente adelanta al voltaje en un capacitor en 90°
- La corriente y el voltaje están en fase en un resistor.

Con ayuda de estos datos se construye el diagrama fasorial y el triángulo de voltajes.
De estos gráficos de obtiene la magnitud y ángulo de la fuente de alimentación (ver fórmulas anteriores):
A la resistencia total del conjunto resistor-capacitor, se le llama impedancia (Z) (un nombre más generalizado) y Z es la suma fasorial (no una suma directa) de los valores del resistor y de la reactancia del capacitor. La unidad de la impedancia es el "ohmio".
La impedancia (Z) se obtiene con ayuda de la siguiente fórmula:

donde:
- Vs: es la magnitud del voltaje
- Θ1: es el ángulo del voltaje
- I: es la magnitud de la corriente
- Θ2: es el ángulo de la corriente
- Vs: es la magnitud del voltaje
- Θ1: es el ángulo del voltaje
- I: es la magnitud de la corriente
- Θ2: es el ángulo de la corriente
¿Cómo se aplica la fórmula?
La impedancia Z se obtiene dividiendo directamente Vs e I y el ángulo (Θ) de Z se obtiene restando el ángulo de I del ángulo Vs.

El mismo triángulo de voltajes se puede utilizar si a cada valor (voltajes) del triángulo lo dividimos por el valor de la corriente (corriente es igual en todos los elementos en una conexión serie), y así se obtiene el triángulo de impedancia
Nota: lo que está incluido en paréntesis elevado a la 1/2, equivale a la raíz cuadrada.
Circuito RC En Paralelo
En un circuito RC en paralelo el valor de la tensión es el mismo en elcondensador y en la resistencia y la corriente (corriente alterna) que la fuente entrega al circuito se divide entre la resistencia y el condensador. (It = Ir + Ic)
Ver el primer diagrama abajo.
La corriente que pasa por la resistencia y la tensión que hay en ella están en fase debido a que la resistencia no causa desfase.
La corriente en el capacitor está adelantada con respecto a la tensión (voltaje), que es igual que decir que elvoltaje está retrasado con respecto a la corriente.
Como ya se sabe el capacitor se opone a cambios bruscos de tensión.


La magnitud de la corriente alterna total es igual a la suma de las corrientes por los dos elementos y se obtiene con ayuda de las siguientes fórmulas:
- Magnitud de la corriente (AC) total:
It = (Ir2 + Ic2)1/2
It = (Ir2 + Ic2)1/2
- Angulo de desfase:
Θ = Arctang (-Ic/Ir)
Θ = Arctang (-Ic/Ir)
Ver el siguiente diagrama fasorial decorrientes:

La impedancia Z del circuito en paralelo se obtiene con la fórmula:
¿Cómo se aplica la fórmula?
Z se obtiene dividiendo directamente V e I y el ángulo (Θ) de Z se obtiene restando el ángulo de I del ángulo V. Este ángulo es el mismo que aparece en el gráfico anterior y se obtiene con la formula: Θ = Arctang (-Ic/Ir)
Nota: lo que está incluido en paréntesis elevado a la 1/2, equivale a la raíz cuadrada.
Circuito RLC En Serie
En un circuito RLC en serie la corriente (corriente alterna) que pasa por la resistencia, el condensador y labobina es la misma y...
La tensión Vac es igual a la suma fasorial de la tensión en la resistencia (Vr) y la tensión en el condensador (Vc) y la tensión en la bobina VL.
Vac = Vr+Vc+VL
(suma fasorial)
(suma fasorial)
La impedancia total del circuitoanterior es: ZT = R + XL + XC (sumavectorial) ó
R + j(XL - XC) ó R + jX

donde:
XC = reactancia capacitiva
XL = reactancia inductiva
R = valor del resistor
X = la diferencia de XL y XC. (Si X es positivo predomina el efecto inductivo. Si X es negativo predomina el efecto capacitivo.
XC = reactancia capacitiva
XL = reactancia inductiva
R = valor del resistor
X = la diferencia de XL y XC. (Si X es positivo predomina el efecto inductivo. Si X es negativo predomina el efecto capacitivo.
La corriente en el circuito se obtiene con laLey de Ohm:
I = V/Z = Vac/ZT = Vac/( R + jX)1/2
y el ángulo de fase es: 0 = arctan (X/ R)
Nota: El paréntesis elevado a la 1/2 significa raíz cuadrada.
Circuito RLC En Paralelo
En un circuito RLC que presente los tres elementos conectados en paralelo, la tensión total aplicada al circuito es la misma que la que tenemos en bornes de cada elemento, mientras que la intensidad que circula para cada uno de ellos es distinta y depende de los efectos de la R,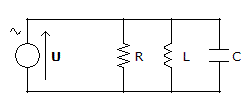 de la L y de la C.
de la L y de la C.
Por tanto, la intensidad que circula por la resistencia está en fase con la tensión aplicada y su valor, que es independiente de la frecuencia, será:
 de la L y de la C.
de la L y de la C.Por tanto, la intensidad que circula por la resistencia está en fase con la tensión aplicada y su valor, que es independiente de la frecuencia, será:
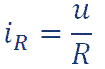
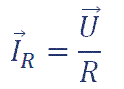
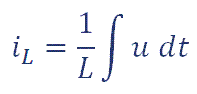
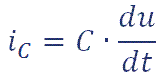
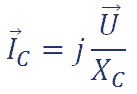
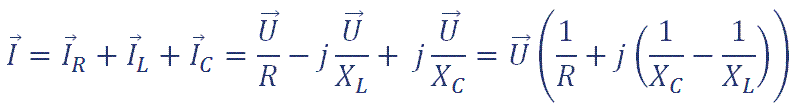
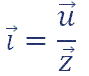
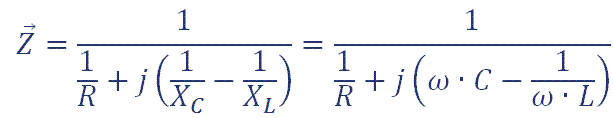
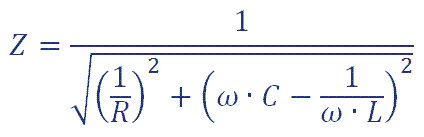
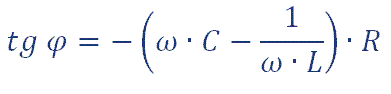
http://es.wikipedia.org/wiki/Corriente_alterna
http://www.asifunciona.com/electrotecnia/ke_corriente_alterna/ke_corriente_alterna_2.htm
http://www.ecured.cu/index.php/Amplitud_de_la_corriente_alterna
http://html.rincondelvago.com/corriente-alterna_2.html
http://www.nichese.com/alter-magni.html
http://www.asifunciona.com/electrotecnia/ke_factor_potencia/ke_factor_potencia_4.htm
http://es.wikipedia.org/wiki/Factor_de_potencia#Mejora_del_factor_de_potencia
http://es.wikipedia.org/wiki/Potencia_el%C3%A9ctrica#Potencia_aparente
http://www.unicrom.com/Tut_circuitoRL.asp
http://www.unicrom.com/Tut_circuitoRLparalelo.asp
http://www.unicrom.com/Tut_circuitoRLparalelo.asp
http://www.unicrom.com/Tut_circuitoRCParalelo.asp
http://www.unicrom.com/Tut_circuitoRLC.asp
http://es.wikipedia.org/wiki/Valor_eficaz
http://es.wikipedia.org/wiki/Factor_de_potencia
http://es.wikipedia.org/wiki/Valor_eficaz
http://es.wikipedia.org/wiki/Factor_de_potencia
Jueves,11 De Septiembre 2014
EVIDENCIAS
CRUCIGRAMA
CONDUCTORES Y AISLANTES
AISLANTE
CONDUCTOR
TEST
PREGUNTA 1
PREGUNTA 2

































No hay comentarios:
Publicar un comentario